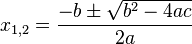Mathe -.-

[Thedynamike]

Hm, da brauchste doch gar keine großen Formeln auswendig zu können, oder? Bissl Umformen reicht da:

0 = x² - 5x + 2,25
<=> 0 = x² - 5x + 6,25 - 6,25 + 2,25 [Füge hier eine konstruktive 0 ein]
<=> 0 = (x - 2,5)² - 6,25 + 2,25 [Binomische Formel rückwärts]
<=> 0 = (x - 2,5)² - 4
<=> 0 = (x - 2,5 + 2)(x - 2,5 - 2) [Die -4 ins binom holen]
<=> 0 = (x - 0,5)(x - 4,5)

=> 0 = 0,5 denn (0,5 - 0,5) = 0 und 0 * (x - 4,5) = 0 [neutrales Element der Multiplikation]
ODER
=> 0 = 4,5 denn (4,5 - 4,5) = 0 und (x - 0,5) * 0 = 0 [neutrales Element der Multiplikation]

Wenn du fragen hast, schreib gerne ne PN oder frag direkt hier.
Hoffe ich konnte dir helfen.

(Btw. merk dir das verfahren, das hilft, wenn du, so wie ich, schnell Formeln vergisst. Konnte mir den pq-Krempel bis heute nicht merken.)

 

[Agyros]

Also Mitternachtsformel ist ein Begriff, der offensichtlich v.a. im Süden in den letzten paar Jahren aufgetaucht ist. Woher der kommt, kann ich nicht sagen.

Und unsere Lehrerin in der 13ten hat immer gemeckert, wenn wir die pq-Formel benutzt haben, die hat alles mit Vieta gemacht. ^^

Ahh, ja. Ich komme ja mehr aus dem Norden Deutschlands, dann wundert mich das nicht mehr

An der FH hatten wir auch so nen Vieta Fanatiker als Prof. Das war neben seiner Vorliebe für total unsinnige Beweise wohl sein Spezialgebiet.

 

[Thorrak Dun Morogh]

Also Mitternachtsformel ist ein Begriff, der offensichtlich v.a. im Süden in den letzten paar Jahren aufgetaucht ist. Woher der kommt, kann ich nicht sagen.

Naja, Süden passt ja in etwa (Bayern), aber ich hab die Formel vor über 10 Jahren unter diesem Namen gelernt. Laut meinem Lehrer damals, sollte man diese Formel jederzeit und überall aufsagen können, eben auch wenn man um Mitternacht aus dem Teifschlaf geweckt wird.

 

[iggeblackmoore]

Naja, Süden passt ja in etwa (Bayern), aber ich hab die Formel vor über 10 Jahren unter diesem Namen gelernt. Laut meinem Lehrer damals, sollte man diese Formel jederzeit und überall aufsagen können, eben auch wenn man um Mitternacht aus dem Teifschlaf geweckt wird.

Richtig

und umformern ist schwachsinnig....
pq-Formel muss sitzen.

 

[Thedynamike]

und umformern ist schwachsinnig....
pq-Formel muss sitzen.

Da die pq-Formel natürlich immer auf eine Lösung kommt, vorallem wenn die Nullstellen im komplexen liegen.

 

[Night falls]

Im Zweifelsfall einfach durch Derive o.ä. jagen

 

[Evíga]

Ich hatte irgendwann mal ein c++-Proggi geschrieben, das die Formel für gegebenes a, b und c berechnet. Wenn da Interesse bestet.. xD

 

[Night falls]

Naja, wenn man die Mitternachtsformel kennt, kann man das auch einfach so machen - ohne Programm

 

[Oonâgh]

Sowas nenne ich klugscheißern ;D,

Ich weiss, ich dachte nur, wo mein Mathelehrer immer komplett auf Vollständigkeit gesetzt hat, kann es (wenn man die Formel möglicherweise auch später noch anwenden will) nicht schaden.
Der Begriff Mitternachtsformel sagte mir allerdings garnichts.. NRW scheint nun auch nicht allzu südlich zu sein^^

Grüssle

 

[dalai]

Einfach die ABC-Formel oder wie die heisst nehmen, wenn du auf der einen Seite der Gleichung 0 hast.

Aber je nachdem wo du in die Schule gehst, lehrst du eine andere Formel. Die ABC-Formel iost mehr in der Schweiz, die PQ-Formel in Deutschland und Österreich und die Amerikaner haben sowieso ihr eigenes System bei dem kein Europäer nachkommt.
Du gewöhnst dich einfach an eine Formel und findest die anderen dann Scheisse

 

[Macta]

Ich müsste es eig. noch können, habe
aber keine Ahnung -.-

Also Probleme bereitet diese Aufgabe:
(2x²-x-10)(2x-5)=0
Ich würde mal stark vermuten, dass man irgendwas mit
der pq-Formel machen muss.
Ich habe es immerhin schon ausgerechnet:
4x³-12x²-15x+50.
Ich habe irgendwas in einem anderen Forum, bei einer
anderen Aufgabe gelesen, dass man den Term
durch x+1 teilt? Da würde rauskommen:
4x²-16x-15+50/x
Wie soll man da eine pq-Formel anwenden?

Hoffe Ihr könnt helfen.

Ach ist nicht meine Aufgabe, ich sollte sie nur für jem. lösen,
da ich in meiner Klasse der beste bin, was nicht schwer ist.
Vollständige Induktion ist kein Ding, aber das...
Blackout

 

[Klunker]

da es ja jetzt verschoben wurde, ist dieser post auch sinnlos =)

 

[Falathrim]

Hab gerade Lust drauf

Aber 0% Garantie obs richtig ist...bin auch müde und so...

Was genau willst du da überhaupt ausgerechnet haben? Die Nullstellen? Das wäre dann über eine Polynomdivision.
Da brauchst du am Besten einen Grafikfähigen Taschenrechner oder ein CAS. Damit suchst du dir eine Nullstelle.

4x³-12x²-15x+50 = f(x)

Geben wir das ein haben wir unsere erste NS durch probieren (alternativ 1. 2. (3) bzw. -1. -2. -3 für x einsetzen...da ist meistens eine Nullstelle dann. In diesem Fall haben wir eine bei -2.

Also x(1)= (-2)

Dann stellen wir unsere Polynomdivision auf, die dann so aussieht:
Das Vorzeichen des -2 wird umgedreht, also
(4x³-12x²-15x+50) : (x+2) = 4x²-20x+25
-(4x³+8x²)
------------
-20x²-15x
- (-20x²-40x)
------------------
25x+50
- (25x+50)
------------------------
0


Damit haben wir dann unsere Gleichung die wir zur pq-Formel machen können. Und dann das Stadardverfahren
4x²-20x+25 = 0 |:4
x²-5x+(25/4) = 0

p = -5 , q = (25/4)

-(-5/2) +/- &#8730;-(5/2)²+(25/4) = x2/x3
2,5 +/- &#8730;6,25+(25/4) = x2/x3
2,5 +/- &#8730;12,5 = x2/x3
2,5 +/- 3,54 = x2 = 6,04 v x3 = -1,04

Wie gesagt, keine Garantie für JEGLICHE Richtigkeit, mir kommts sogar ziemlich falsch vor, aber das wichtigste war ja eh die Polynomdivision, den Rest darfst nochmal selber nachprüfen, so schwer is die pq-Formel nicht.

Die Lösungen sind übrigens falsch ;D

 

[Macta]

Ary, aber das mit der Nullstelle nicht -.-

Muss man die einfach durch raten rauskriegen, also man setzt -2 für x ein
und rechnet es aus oder wie läuft das?

Unsere Mathelehrerin hat da wohl gepennt.

 

[Falathrim]

Naja wenn du nen GTR hast (Grafikfähigen Taschenrechner) kannst dus dir anzeigen lassen und das dann nachprüfen. Im Allgemeinen ist es aber so, dass in Matheaufgaben in der Schule immer Nullstellen zwischen -3 und 3 sind, seltenst Kommazahlen. Also kannst dus einfach einsetzen und damit rechnen dass du irgendwann auf 0 kommst, also ne Nullstelle hast. Und dann machst du eben die Polynomdivision mit der Nullstelle die du berechnet hast, nur eben mit x und umgedrehtem Vorzeichen.

Aber da ihr das nicht wisst, gehe ich davon aus dass das sozusagen eine pädagogische Matheaufgabe ist, die dann nächste Stunde aufgelöst wird, also dass ihr das Verfahren nächste Stunde lernt und jetzt einfach nur mal grübeln sollt, wies vielleicht geht (kreatives Denken bzw selbstständiges Denken nennt man das...)

So wars auch bei uns vor ein paar Monaten, als wir das Thema bekommen haben.

 

[Thorrak Dun Morogh]

Ich müsste es eig. noch können, habe
aber keine Ahnung -.-

Also Probleme bereitet diese Aufgabe:
(2x²-x-10)(2x-5)=0

Hmm, was falathrim da ausgerechnet hat hab ich nur kurz überflogen. Aber die Lösung von x ist bei der Aufgabe kein Problem: die linke Seite wird dann zu Null, wenn ein Term gleich Null ist.
Also entweder (2x-5)=0 oder (2x²-x-10)=0.

Die erste Lösung ist schnell errechnet, 2,5. Die beiden anderen Lösung ergeben sich aus der Mitternachts- bzw pq Formel, 2,5 und -2.
Also ist endgültige Lösung x1=2,5, x2=-2.

Macht es euch nicht schwerer als es eigentlich ist^^

 

[Falathrim]

owned by person thats good in Maths :/

Ich habs ihm auf dem "Fußweg" erklärt, so wie ichs dieses Jahr gelernt hab...

 

[Macta]

Wie konnte ich nur so blind sein!
Und sowas will einen Leistungskurs nehmen -.-

DANKE!!!

 

[claet]

Vollständige Induktion ist kein Ding, aber das...

Du findest vollständige Induktion einfach, aber bekommst keine Polynomdivision hin?!?

Menschen gibts .. *g*

 

[Macta]

So, nun habe ich erneut eine Frage:

Ich habe zu einer Aufgabe folgende Antwort geliefert:
Es gibt bei einem Mini-Lotto von 7 möglichen Kugel, wovon 3 gezogen werden,
35 Möglichkeiten. Also 1/35 = 2,86% zu gewinnen, die Chance zu gewinnen
steht also bei 1 zu 34.

Daraufhin sagte sie, dass das falsch ist, also das 1 zu 34.

Wer hat recht, ich habe es nämlich so gelernt?